5 Применение газовой хроматографии для физико-химических исследований
Определение теплоты и энтропии адсорбции или растворения газохроматографическим методом
В случае идеальной равновесной хроматографии, т.е. когда в хроматографическом опыте практически достигается равновесие и изотерма сорбции является линейной, можно определить теплоту адсорбции или растворения.
В газожидкостной хроматографии измеряемый удельный удерживаемый объем \(V_g\) при постоянстве температуры обладает свойствами физико-химической константы \[ V_g = K_D/\rho, \tag{5.1}\] т.к. определяется константой Генри (коэффициент распределения или угловой коэффициент прямой в координатах \(c_s\)–\(c_m\)) и плотностью неподвижной жидкой фазы \(\rho\).
В случае газоадсорбционной хроматографии обычно пользуются не трудно измеримой концентрацией \(c_m\) данного компонента в объеме \(V_a\) адсорбционного слоя, а количеством адсорбированного вещества единицей массы адсорбента \(a\), которое называется адсорбцией. Значение \(a\) сравнительно легко определяется экспериментально. Наклон линейной изотермы адсорбции в координатах \(c_s\) – \(c_m\) или \(a\) – \(р\) (\(c_m\) и \(p\) — концентрация и парциальное давление адсорбата в газовой фазе) характеризуются соответственно коэффициентами адсорбции \(K_{a,c}\) или \(K_{a,p}\). Эти коэффициенты и удельный удерживаемый объем связаны следующим соотношением:
\[ V_g = K_{a,c} = K_{a,p}RT. \tag{5.2}\]
В идеальном случае (равновесная и линейная хроматография) удельный удерживаемый объем не зависит от концентрации, а время удерживания не зависит от величины пробы.
Коэффициент распределения и коэффициент адсорбции — термодинамические константы фазового равновесия, связанные с величиной свободной энергии (энергии Гиббса) процессов адсорбции и растворения: \[ \begin{aligned} \Delta G_a &= -RT\ln K_{a,p},\\ \Delta G_s &= -RT\ln K, \end{aligned} \tag{5.3}\]
Свободная энергия Гиббса, в свою очередь, по определению связана с изменениями энтальпии и энтропии процессов: \[ \begin{aligned} \Delta G_a &= \Delta H_a - T\Delta S_a,\\ \Delta G_s &= \Delta H_s - T\Delta S_s\\ \end{aligned} \tag{5.4}\]
В этих условиях \(\Delta G_a\) и \(\Delta G_s\) — свободные энергии адсорбции и растворения соответственно, т.е. свободные энергии перехода вещества из одной фазы (подвижной) в другую фазу (неподвижную) и наоборот; \(R\) и \(T\) — универсальная газовая постоянная и абсолютная температура хроматографической колонки, при которой измерен удельный удерживаемый объем сорбата; \(\Delta H_a\), и \(\Delta H_s\) — энтальпии адсорбции и растворения, соответственно, численно равные термохимическим теплотам адсорбции и растворения, но с обратным знаком (\(-\Delta H_a = Q_a\) и \(-\Delta H_s = Q_s\)); \(\Delta S_a\) и \(\Delta S_s\) - энтропии адсорбции и растворения, соответственно.
Приравнивая правые части уравнений (5.3) и (5.4), после простых преобразований получим уравнение Гиббса-Гельмгольца в приложении к процессам адсорбции или растворения:
\[ \begin{aligned} &\ln K_{a,p} = -\frac{\Delta H_a}{R}\cdot\frac{1}{T} + \frac{\Delta S_a}{R},\\ &\ln K = -\frac{\Delta H_s}{R}\cdot\frac{1}{T} + \frac{\Delta S_s}{R}. \end{aligned} \tag{5.5}\]
Величины \(K\) и \(K_{a,p}\) просто рассчитать по уравнениям (5.1) и (5.2) из удельных объемов удерживания, которые определяют из ряда хроматографических опытов, проведенных при различных температурах колонки в изотермическом режиме. При точных измерениях следует вносить поправку на перепад давления в колонке \(f_i\), температурную поправку \(f_2\), и поправку на давление пара воды в реометре \(f_3\) и рассчитывать истинный удерживаемый объем \(V_R'\) по формуле
\[ V_R' = F_o\cdot(t_R-t_0)\cdot f_1 \cdot f_2 \cdot f_3 = F_o\cdot(t_R-t_0)\cdot \frac{3}{2}\frac{\left(p_i/p_o\right)^2-1}{\left(p_i/p_o\right)^3-1}\cdot\frac{T_c}{T_\text{комн}}\cdot\frac{p_o-p_\ce{H2O}}{p_o}. \tag{5.6}\]
Для определения удельного удерживаемого объема \[ V_g = V_R'/m_s \tag{5.7}\] при заданной контролируемой температуре \(T_c\) в хроматографическую колонку с известным количеством сорбента вводят неизменную по величине во всех опытах пробу изучаемого сорбата, записывают хроматограмму и определяют время удерживания \(t_R\). Кроме того, контролируют давление на входе в колонку \(p_i\), расход газа \(F_o\) и давление на выходе из колонки (атмосферное давление) \(p_o\), температуру пенного реометра (комнатную температуру) \(T_\text{комн}\) и находят по справочнику соответствующее этой температуре давление паров воды \(p_\ce{H2O}\).
Объединяя уравнения (5.5) и (5.1) или (5.2), получим:
\[ \begin{align} \ln V_g &= -\frac{\Delta H_a}{R}\cdot\frac{1}{T} + \frac{S_a}{R} + \ln RT,\\ \ln V_g &= -\frac{\Delta H_s}{R}\cdot\frac{1}{T} + \frac{S_s}{R} + \ln RT, \end{align} \tag{5.8}\] или \[ \begin{align} \ln V_g &= \frac{Q_a}{R}\cdot\frac{1}{T} + \frac{S_a}{R} + \ln RT,\\ \ln V_g &= \frac{Q_s}{R}\cdot\frac{1}{T} + \frac{S_s}{R} + \ln RT. \end{align} \tag{5.9}\]
Так как величины \(\Delta H\) и \(\Delta S\) мало зависят от температуры, то в небольшом температурном интервале уравнения (5.8) и (5.9) можно рассматривать как уравнения прямой \(y = ax + b\) со следующими параметрами:
- \(y = \ln V_g\);
- \(x = 1/T\);
- \(a = -\Delta H/R = Q/R\);
- \(b = \Delta S/R + \ln RT\).
Из углового коэффициента \(a\) полученной прямой можно вычислить теплоту адсорбции \(Q_a = -\Delta H_a\), или теплоту растворения \(Q_s = -\Delta H_s\), а по численному значению отрезка, отсекаемого прямой на оси ординат и равного \(\Delta S/R + \ln RT\), — энтропию адсорбции \(\Delta S_a\), или энтропию растворения \(\Delta S_s\).

Более точно энтропию можно рассчитать по уравнениям \[ \begin{align} \Delta S_a &= (\Delta H_a - \Delta G_a)/T,\\ \Delta S_s &= (\Delta H_s - \Delta G_s)/T \end{align} \] после того, как графически описанным способом определена теплота процесса, а по уравнениям \[ \begin{align} -\Delta G_a &= RT\cdot\ln\frac{V_g}{RT},\\ -\Delta G_s &= RT\cdot\ln V_g\rho \end{align} \] рассчитана свободная энергия адсорбции или растворения, соответственно.
Производя расчеты, следует обратить внимание на соблюдение размерности измеряемых величин: [\(V_g\)] = см/г; [\(T\)] = K; [\(\Delta G\)] = [\(\Delta H\)] = Дж/моль; [\(\Delta S\)] = [\(R\)] = Дж/моль·К; \(K\) и \(K_{a,p}\) — величины безразмерные.
При нелинейной изотерме адсорбции и несимметричных хроматографических пиках расчет теплоты по положению максимумов пиков проводить нельзя даже при одинаковых пробах, так как величина заполнения поверхности адсорбента при разных температурах может быть разной; т.е. нарушается условие опыта, при котором величина адсорбции постоянна.
При несимметричных хроматографических пиках рекомендуется определить изотермы адсорбции в координатах \(a\)–\(p\) при разных температурах, а по ним рассчитать изостерические (при постоянной величине адсорбции) теплоты по зависимости \(\lg p\) от \(1/T\). По полученным изотермам адсорбции при разных температурах можно рассчитать и зависимость изостерической теплоты адсорбции от степени заполнения.
Лабораторная работа №3. Определение энтальпии и энтропии растворения вещества в неподвижной жидкой фазе
В работе определяются термодинамические параметры растворения вещества в неподвижной жидкой фазе (SE-30).
Выполнение работы
По указанию преподавателя устанавливают минимальную температуру термостата колонки (обычно 60–80℃) и объёмную скорость газа-носителя (обычно в интервале 20–60 мл/мин).
После выхода хроматографа на рабочий режим записывают в таблицу значения давления газа-носителя (\(p_i\)) на входе в колонку и объёмной скорости газа-носителя на выходе из колонки (\(F_o\)), измеренную с помощью мыльно-плёночного или электронного измерителя расхода.
Вводят в испаритель хроматографа 0.1 мкл исследуемой жидкости и запускают запись хроматограммы.
По хроматограмме определяют и заносят в таблицу времена выхода неудерживаемого компонента (\(t_0\)) и исследуемого вещества (\(t_R\)).
Повторяют измерения при более высоких температурах (3–4 раза), каждый раз повышая температуру термостата колонок на 5–10℃.
Результаты измерений заносят в таблицу:
Атмосферное давление, \(p_o\):
Температура в помещении \(T_\text{комн}\):
Масса сорбента или НЖФ, \(m_s\):
| # | \(T_c\), ℃ | \(p_i\), МПа | \(F_o\), мл/мин | \(t_0\), мин | \(t_R\), мин | \(1/T_c\), K−1 | \(V_g\), мл/г | \(\ln V_g\) |
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 |
Расчёты
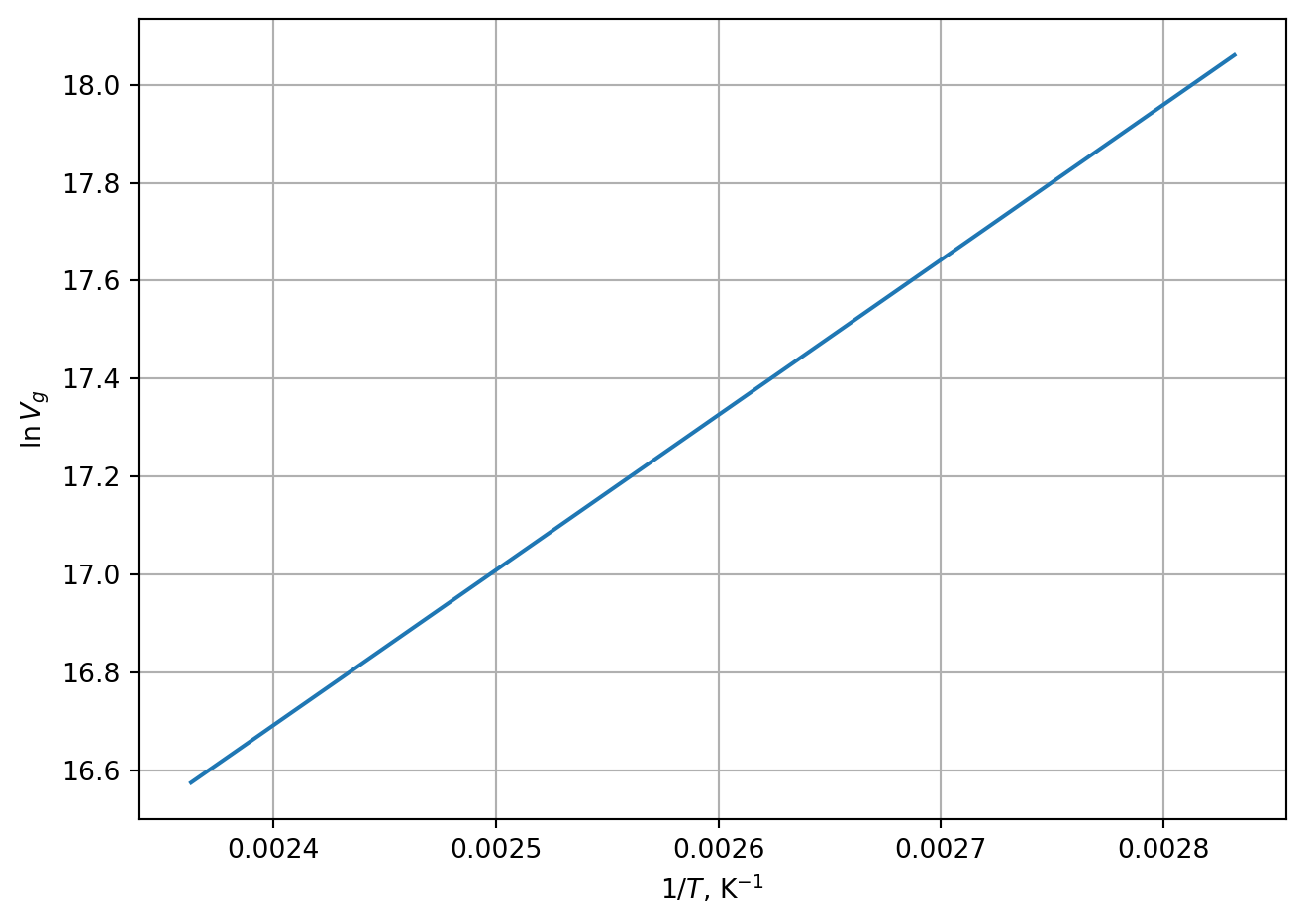
Расчёт значений удельных удерживаемых объёмов производят по уравнениям (5.6) и (5.7). При использовании электронного измерителя расхода газа поправку на давление паров воды в уравнении (5.6) не применяют. Расчёты термодинамических параметров растворения вещества выполняют графоаналитическим способом по уравнениям (5.8) и (5.9). Строят график зависимости \(\ln V_g\) от \(1/T_c\) для всех полученных точек, по графику определяют параметры прямой и рассчитывают значения энтальпии и энтопии растворения вещества в НЖФ.